Spatial Filter
This BeamLab demo shows how a spatial filter consisting of a lens and pinhole removes fluctuations in the intensity profile of a Gaussian beam. An unperturbed Gaussian beam picks up phase fluctuations by passing through a thin screen where small particles are randomly distributed over a finite area approximately within the beam width and aberrate the beam’s wavefront. The beam is then focused by a lens and spatially filtered at the lens’ focal plane by a metal pinhole with a diameter of 25 µm and a thickness of 50 µm. Finally, the filtered beam is collimated by another lens.
BeamLab demo: spatial_filter.m
The following figure shows the amplitude and phase transfer functions of the thin screen with randomly distributed particles.
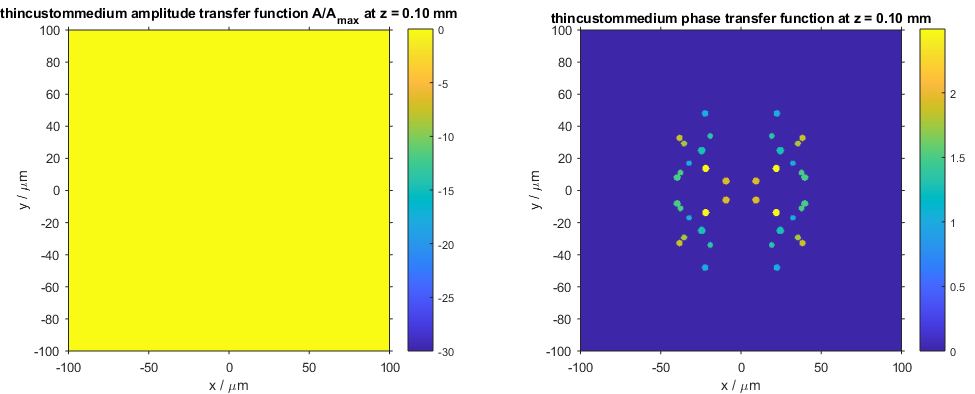
Amplitude and phase transfer functions of the thin screen with randomly distributed particles
The following video shows how the intensity distribution changes along the propagation distance z. The figure shows two-dimensional intensity distribution I(x,y) normalized to the input intensity and displayed on a logarithmic scale.
Video of the intensity profile of the beam propagating in the spatial filter
After the calculation has finished, the intensity distribution as a function of propagation distance z is plotted. The figure below shows the intensity distribution I(x,z) at y = 0 µm. Thin lenses are used to focus and collimate the beam. The solid white lines indicate the locations of the pinhole while the dashed white lines show the location of the thin lenses and thin phase screen.
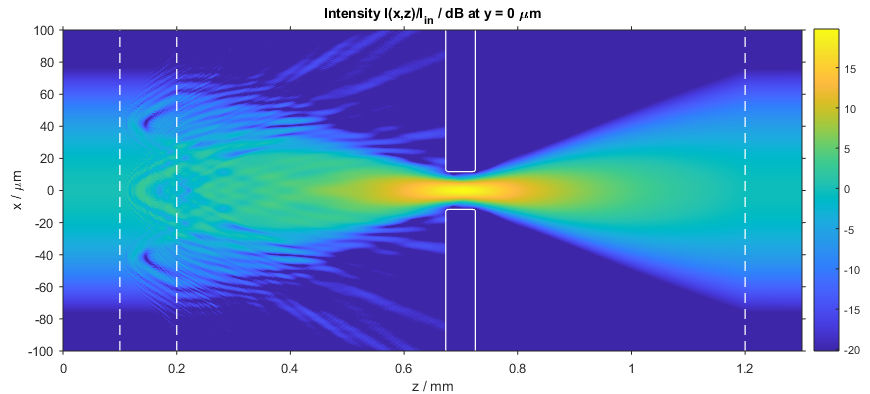
Intensity distribution in the spatial filter (x–z slice)
The following two figures show the intensity distributions at the input and output planes.
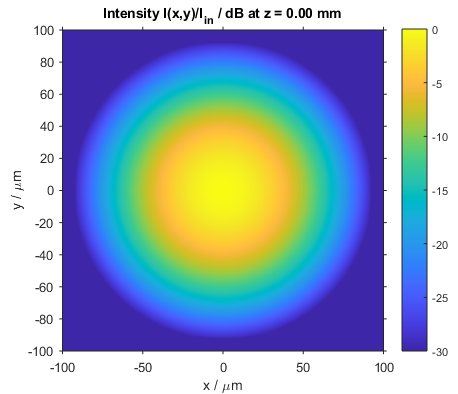
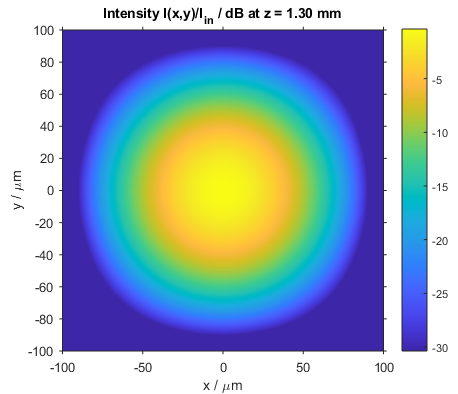
Intensity distributions in the input (left) and output (right) planes (x–y slices)
About BeamLab
BeamLab is an award-winning set of simulation tools for beam propagation through optical devices and waveguides in your familiar MATLAB® environment. It offers a high flexibility in waveguide design and post-processing of any output data.

